Science Daily August 5, 2020
The volume of data, inadequate computational resources to handle an oversized problem, security and privacy concerns are some of the challenges in solving large-scale linear inverse problems (LIP). Researchers at Washington University have developed the parallel residual projection (PRP), a parallel computational framework involving the decomposition of a large-scale LIP into sub-problems of low complexity and the fusion of the sub-problem solutions to form the solution to the original LIP. They analyzed the convergence properties of the PRP and accentuate its benefits through its application to complex problems of network inference and gravimetric survey. They showed that any existing algorithm for solving a LIP can be integrated into the PRP framework and used to solve the sub-problems while handling the prevailing challenges…read more. Open Access TECHNICAL ARTICLE
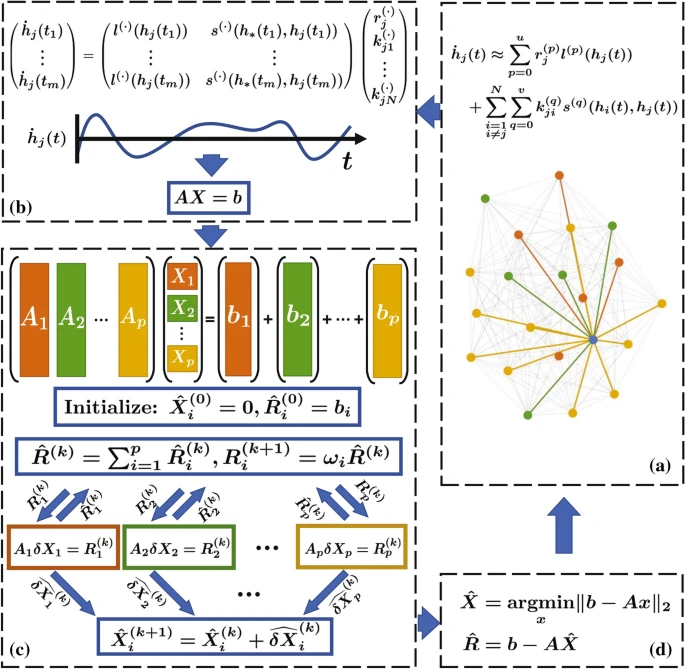
The PRP algorithm decomposes solving the linear inverse problem into p linear inverse sub-problems… Credit: Scientific Reports volume 10, Article number: 12846 (2020)